Gauss-Bonnet公式
其实它的通俗说法是咱们在初中就学过了的“三角形内角和等于180度”的推广。记得老师那会提到过非欧几何,就是说如果不满足第五公设“过直线外一点只能做一条直线与已知直线平行”,那么三角形内角和就不等于180度。
我以前曾经介绍过,最简单而容易理解的二维情形就是在一个球面上,球面上任意两条“直线”(实际上是球的两个大圆,这里直线定义就是球面上两点间最短的距离延伸而成的线)都不平行,相交于两点。
以地球表面为这个考察面,东经90度线,零度经线和赤道三条“直线”(实际上在地面上的确认为他们是直线)围成一个球面三角形,在极点的夹角是90度,在赤道的两个夹角也都是90度,所以这个球面三角形的内角和是90+90+90=270度大于180度。Gauss-Bonnet公式就是说这个问题,在一个流形上的多边形的外角和,与这个流形本身的曲率(也就是弯曲程度),还有流形的拓扑结构(以欧拉示性数表示)这三者之间存在一个关系,也就是给定一个流形的曲率和结构,用这个公式我就可以算出在它上面三角形内角和是多少。这个公式称为广义高斯-伯内特公式的原因是,高斯研究过比较简单的情形(那时候还没有流形的概念)。陈省身给出的是一个通用的式子,最漂亮的是,他的公式的适用范围极广而形式又极度简洁,公式左边只有一项右边只有一项(三角形的内角和只是其中一种特殊情形下的特例),这种极度的简洁与和谐,可以和物理上爱因斯坦的质能方程E=mc*c相媲美。
------
4月17日补充:

上面给的等式就是Gauss-Bonnet公式,左边的K是黎曼曲率,等式右边是流形的欧拉示性数,也就是表示流形整体的拓扑结构的数。所以这个公式的意义是把局部的性质(局部的曲率)和整体的拓扑属性联系起来了。
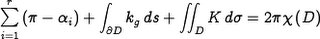
对于有边界的情形,就变成第二个公式,对于二维平面上的封闭三角形,欧拉示性数为1,曲率为零,所以就很容易得到三角形内角和的关系了。

0 Comments:
Post a Comment
<< Home