Painleve猜想与《天遇》

杨振宁在访问南京大学的时候曾经说:“南京大学在世界上有两个最杰出的校友,一个是做数学的,一个是搞天文的。”他说的前一个校友是指田刚,田刚是南大的本科毕业,北大的硕士毕业。至于第二个人,叫做夏志宏,夏志宏1982年南大天文系本科毕业,1988年美国西北大学数学系博士毕业。
夏志宏虽然说起来是做天体物理的,实际上他所解决的是一个天体物理中的数学问题。对于万有引力的天体系统,2体问题是最容易的,已经证明2体问题的轨道一定是圆锥曲线。3体以上,由于万有引力的非线性性质,问题变得特别复杂。关于N体问题的运动,有一个著名的Painleve猜想,这个猜想在数学界悬了一百多年没人解决。夏志宏在读博士期间,证明了Painleve猜想在N大于4的情况,顿时轰动了世界。
数学上的难题,证明需要耗费的精力就非常可怕,还有一件很枯燥而且费力不讨好的工作就是对证明的评审。夏志宏证明的过程有几百页,他送到最权威的数学杂志“数学年刊”。证明送去以后,他的稿子被审了两年,回复意见是:“我们无法确定你的证明有没有错误。”实际上就是找不到人来审。夏志宏就对证明过程进行了整理,增加了很多细节,又投一次。总算是运气挺不错,普林有一个叫做John Marther的教授听说了这件事情,他提出来他可以审这个证明,Marther在普林组织了一个讨论班,专门讨论夏志宏证明过程。讨论班结束后,Marther给了个评审意见:夏志宏的证明是正确的。
夏志宏目前是美国西北大学教授,北京大学长江学者。目前夏志宏是微分动力系统方面世界公认的权威之一。有一本关于微分动力系统和非线性动力学的科普读物《Celestial Encounts》( 《天遇》),作者是Diacu,本书的校订者叫Philips Holmes,是非线性动力学方面的大牛,现在是普林斯顿应用数学系和航空工程系的教授。这本书里很详细的介绍了夏志宏的经历和夏志宏的解。Philips Holmes是个赤面白发,特别有活力的一个老头。好像他本来是康乃尔大学的教授,被普林斯顿给挖过来了。hehe,我们系有一个给研究生的讨论班,我们的系主任要我们系的同学们点将,我们就点了他,来做非线性动力学的报告。他做报告之前给我们发了一个材料,实际上是他以前一些东西的复印件,当时我看到署名下是康乃尔大学,还以为他是康乃尔大学的。那时候还奇怪呢,怎么康乃尔大学的教授跑到这里来为研究生上课,后来才知道是一个大误会。Holmes很有意思,给我们做报告的时候,为了说明非线性运动的复杂性,他拿了一个复摆模型到我们实验室。这老头写书的本事也极棒,非线性动力学领域有三本权威著作,其中一本《湍流,相干结构,动力系统与对称》就是他主笔的。有他校对《天遇》这本书质量是绝对没问题的,国内已经有了翻译本,2001年出版的。题图就是 《天遇》的封面,那上面第二排第四幅图就是夏志宏的非碰撞奇异解的图示。
----------
4月17日补充:
关于夏志宏的证明,这里可以给一个简单的介绍。Painleve证明,对于3体问题,所有的奇异解都是碰撞解,也就是说三体问题中,在有限时间里达到发散的解(就是说距 离达到无穷远,有一个名字叫blow up),必然会有粒子撞到一起去。猜想的内容是对于N体问题的:对于N大于等于4的问题,系统存在非碰撞奇异解。夏志宏对于N=5的情形,构造了一个非碰撞的奇异解。并且说明,用类似的方法可以构造出对于n>5的情形。
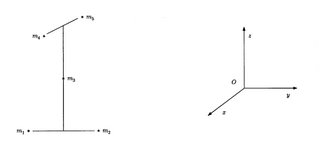
这个解的形式是这样的,考虑五个粒子的系统,其中m1和m2等质量,m3和m4等质量,然后构造初始条件,使m1和m2,m3和m4分别关于z轴对称,m5始终在z轴上,这样的一个系统,夏志宏证明可以构造出来特定的解,在有限的时间里不发生碰撞而使得m1和m2的z方向投影,m3和m4的z方向投影趋向无穷大。他的思想是,m1和m2在同一个x-y平面的椭圆上运动,m3和m4在另外一个x-y平面的椭圆上运动,可以构造系统初始条件,使得m5运动到m1-m2平面的时候,m1和m2正好到达距离z轴最近的地方,产生一个近乎三重碰撞的情形,于是m5被加速。再运动到m3-m4平面的时候,又发生类似的近乎三重碰撞,于是m5不断被加速,两个平面的垂直距离也在有限时间里被推到无穷远。
题图II截自夏志宏发表在数学年报上的文章(点击可以看大图):
The Existence of Noncollision Singularities in Newtonian Systems, by Zhihong Xia, Annals of Mathematics, 135(1992),411-468

0 Comments:
Post a Comment
<< Home